 Weber
and contrast ratios
Weber
and contrast ratiosaccording to Timo
 Weber
and contrast ratios
Weber
and contrast ratios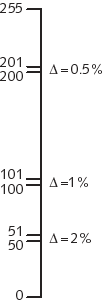
Timo claims that the ability of the visual system to discern intensities - the Weber fraction - is 2%. The step from code 50 to code 51 corresponds to an intensity step of 2%. Codes less than 50 will be liable to exhibit banding (contouring).
Timo insists upon coding linear light, even in 8 bits. If the highest intensity is code 255, then the contrast ratio between white (255) and the darkest code free of banding (code 50) is 5:1. That's equivalent to a contrast ratio limit of 5:1.
If the display contrast ratio was 10:1, then codes as low as 25 could be distinguished from black. But in linear-light intensity coding, the step from code 25 to code 26 is a 4% jump in intensity. This is larger than Timo's Weber fraction, and is bound to be perceptible.
Even if you assume that vision degrades to 4% contrast sensitivity near
black, there is no way that linear light coding in 8 bits will achieve acceptable
performance in viewing environments (or display media having contrast ratios
in excess of 10:1: Eight-bit linear coding cannot work in television, cinema,
projected transparencies in a darkened room, or even high-quality printing.
For Timo, we need to add a row in the table, for contrast ratio 5:1. If
Timo gets acceptable image quality with 8 bit linear light coding, I conclude
that the contrast ratio in his display environment is about five to one.
| Contrast sensitivity | |||
| 2% | 1% | 0.5% | |
| Contrast ratio | |||
| 5 (Timo's environment) |
81 (~6.3 bits) |
||
| 10 (office environment) |
116 (~7 bits) |
231 (~8 bits) |
462 (~9 bits) |
| 30 (living room, television) |
172 | 342 | 682 |
| 100 (cinema theater) |
232 (~8 bits) |
463 (~9 bits) |
923 (~10 bits) |
Timo demands linear-light coding. But equivalent performance could be obtained from a nonlinear system having only 81 codes, easily accommodated in 7 bits.
See also: Gamma FAQ - Linear and nonlinear coding - Weber and contrast ratios - Timo and linear coding
Charles Poynton - color links - Gamma FAQ - Linear
and nonlinear coding
Copyright © 1998-03-11